직각이 아닌, 예각인 한 각을 기준으로 보는 비율

셋타나, 동경의 이동하여 예각이든, 직각이든, 둔각이든 되는게 중요한게 아니라,
r, x y 길이 간의 비례식이 중요한 것이다.
그러니 일반각 셋타가 뭔든지 상관없다 하는 것이고, r값도 상관이 없는게
x가 0이 아니고서야 r 값이 커지면 알아서 x,y 좌표도 더 커지고 하는 등
알아서 서로의 길이간 비례식을 맞춰줄 뿐임.
그래서 보통 r을 1로 봄
삼각함수는 사인함수가 y/r , 코사인 함수가 x/r , 탄젠트 함수가 y/x (x는 0이 아)
이것만 암기하면 된다.
그 각이 뭐든 상관없으니 (r,x,y의 비례에는 영향이 없기에) 기억도 예각일 때로 편하게 기억하면 됨.

나도 외운 기억은 있지만 기억은 안나는 표. 이걸 암기해야한다.


풀이
1.셋타 각에 180만 곱해주면 각도가 나온다.
2. 둔각보단 예각으로 다시 바꿔서 삼각형을 재배치
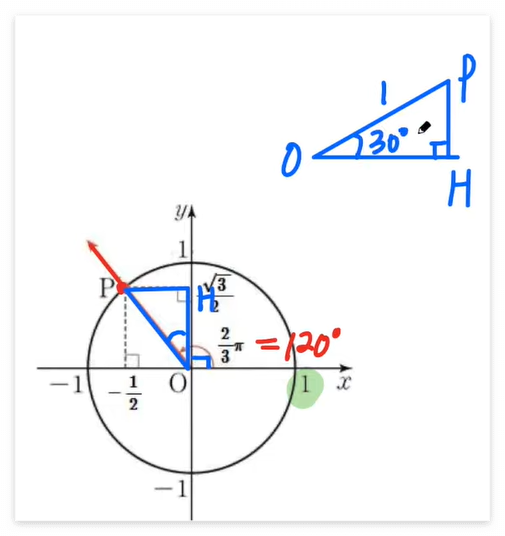
3. sin 30 = 1/2 , cos 30 = 루트3/2 , tan 1/ 루트3
즉, x는 -1/2, y는 루트3/2 , r은 1
삼각함수
사인 = y/r 루트3/2
코사인 = x/r -1/2
탄젠트 = y/x -루트3
선형대수학하려면 수1, 수2, 미적분, 기하와 벡터 하고서 하면 너무 좋겠지만 현실은 그렇지 않다.
찾아보니 미적분과 선형대수학은 별개의 학문이라 따로 따로 배워도 될 정도이며,
중,고등 수학은 선형대수학의 행렬 때만 필요하고, 나머지는 그대로 선형대수학을 들어도 된다고 한다.
내가 수능 직후 기억이 나는것은 확률과 통계, 행렬 수준. 삼각함수도 그땐 이해를 못한 상태였는데, 정작 수1,수2 에서는 깊게 다루지 않았던 것으로 기억한다. (결국 수능 끝나기 전까지도 이해못햇으니깐)
우선 삼각함수에 대한 기억이 너무 가물가물해서 왔는데...
지금 배우는 스칼라 등을 본 기억이 없는 걸로 봐선 선형대수학 강의만 열심히 들으면 되지 싶다.

'📐선형대수학 > 수1, 수2, 미적분' 카테고리의 다른 글
| 대수학적 특징 (0) | 2024.01.30 |
|---|---|
| 암기필수 내용들 (0) | 2023.02.17 |
| 기하와 벡터를 위한 수학(1)[수1 일반각, 호도법] (0) | 2023.02.17 |