행렬
수를 m행과 n열로 묶어 놓은 것.
m x n 행렬 이라 나타냄.
행렬 계산
행렬이 1라는 것은, 1로만 구성된 행렬이 있다는 것을 의미한다.
(1)합, 차
행과 열이 둘다 일치하는 값들끼리 빼주면 된다.
(ex)
1 2 5 6 1-5 2-6
3 4 7 8 3-7 4-8
(2)스칼라배(상수 곱하기)
(ex)
10(행렬)
행렬의 모든 요소들에 10을 곱해주면 된다.
(3)곱
좌측 m x n 행렬의 '열부분'과, 우측 n x p 행렬의 '행부분'이 일치해야 곱셈이 가능함.
이 명제가 행렬의 곱셈이 이루어지는 필요조건임.
곱셈할 때 좌측은 행들(가로)을, 우측은 열들(세로)을 곰셈해줌
1 2 xi
3 4 xj
5 6
행렬의 종류
주대각선 - 행렬의 왼쪽 위에서 오른쪽 아래를 가르는 선
대각행렬 - 주대각선을 제외하곤 모든 성분이 0인 행렬
대각성분 - 주대각선에 걸치는 행과 열의 지표수가 같은 성분 (a11 a22 a33 a44 ...)
영행렬 - 모든 성분이 0인 행렬
전치행렬 - (aij)에 대해 (aji) 처럼 행과열을 뒤집은 행렬 (a12 -> a21)
정사각행렬 - 행,열의 개수가 같은 행렬
단위행렬 - 모든 대각성분이 1이고 그 외의 성분은 0인 정사각행
행렬의 곱셈은 교환법칙이 성립되지 않는다.
덧셈, 뺄셈은 교환법칙, 결합법칙 모두 성립한다.
연립이차방정식의 미지수 구하기

1번 방식은 계수와 상수 모두 합쳐놓은 행렬을 첨가행렬이라 하고. 가우스 조던 소거법에 이용됨
2번 방식은 계수로만 만든 계수행렬, 상수로만 만든 상수행렬로 나뉜다.
가우스 조던 소거법
3가지의 기본 행 연산을 통해 연립일차방정식의 첨가행렬을
기약 행 사다리꼴로 변환하여 해를 구한다.
1) 한 행을 상수배한다.
2) 한 행을 상수배하여 다른 행에 더한다.
3) 두 행을 맞바꾼다.
가우스 소거법이 행사다리꼴로 만들어주는 것(1의 아래만큼은 무조건 0으로 만들어 줘야한다.)
가우스 + 조던 소거법이 기약 행 사다리꼴로 만들어주는 것(1이 포함된 열에서 나머지 성분을 무조건 0으로 만들어줘야함)

연립방정식처럼 최대한 상수를 각 해에 곱해줘서,
행렬의 열의 1,0 조합을 많이 만들어서 두 상수를 더하거나 빼서 미지수들을 구하는 것과 동일
차이는 행렬로 모양을 만들어주기 위해 첨가행렬 등 여러 행렬들을 사용하는 것일뿐이다.
역행렬을 이용하기(보통 가우스 조던 소거법 사용)

행렬식

행렬식의 예시


소행렬 M
Mij 의미는 예를들어,
M11이 있다면 1행과 1열의 모든 행렬요소를 제외한 나머지 행렬 요소들을 의미한다.
M12가 있다면 1행과 2열을 뺀 모든 행렬요소로 소행렬 생성. 소행렬을 행렬식을 통해 의미있는 값을 구한다.
여인수 전개(Cofactor Expansion)
나머지 인수들의 곱을 합한다
i 행에 관한 여인수 전개
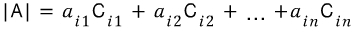
j 열에 관한 여인수 전개
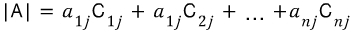
3 X 3 행렬에서 얻을수 있는 여인수 전개를 알아봅시다

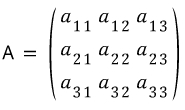
총 6가지 가지의 여인수 전개가 존재합니다.
왜 9개도 아니고 6개일까요?
행이 3개 열이 3개 그래서 6개가 나옵니다.
왜그런지 제가 천천히 설명해보겠습니다.
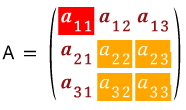
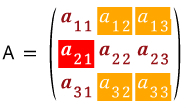
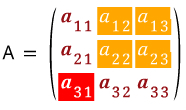
위에 있는 그림은 A 행렬의 1열에 관한 여인자전개 입니다.

이렇게 색으로 표현하면 어떤 것이 Cofactor인지 이해가 되나요 ?
Cofactor가 바로 여인수입니다.
그렇다면 이제 6가지 여인수전개를 모두 표현해보겠습니다.
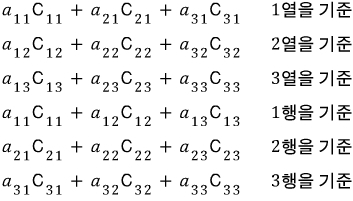
출처: https://blog.naver.com/justant/20208491232
Q문제1
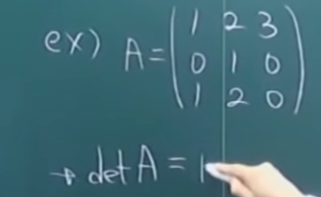
1M - 2M + 3M (위치에 따라 +,- 교차해줌.)
1(1*0 - (2*0)) -2(0*0 - (1*0)) + 3(0*2 - (1*1)) = -3
아래처럼 열기준으로도 가능하며, 같은 결과 값이 나온다.
1(0-0) - 0(-6)+1(-3) = -3
또한 가장 쉬운 3열을 기준으로도 계산이 가능하다.

ㅡ> +,- 가 서로 교차된다는 것만 기억하고, 더 쉬워보이는 쪽으로 행이나, 열을 기준으로 식을 생성해서 구하면 된다.
사우스법칙보단 이 기본식에 익숙해지는게 낫다.
역행렬 구하기

x * ? = 1 일때 ? 값은 x의 역원이라 하고. 1을 항등원이라 함
A행렬에 역행렬을 곱했을 때 나오는 항등원은 행렬에서는 단위행렬이 된다.
암기 필요 공식. (증명해보니 아래처럼 식이 나온다.)

그럼 C행렬은 뭐지?
C11은 A행렬의 A11의 M11 값의 행렬식.
C12는 A행렬의 A12의 M12 값의 행렬식.
C31은 A행렬의 A31의 M31 값의 행렬식.
.
.
쭉쭉 9개가 구해질 것이다. (음수든, 양수든)
그 9개를 위치에 따라 자리별 부호를 곱해줘야 한다.
그렇게 되면 C행렬이 구해진다.

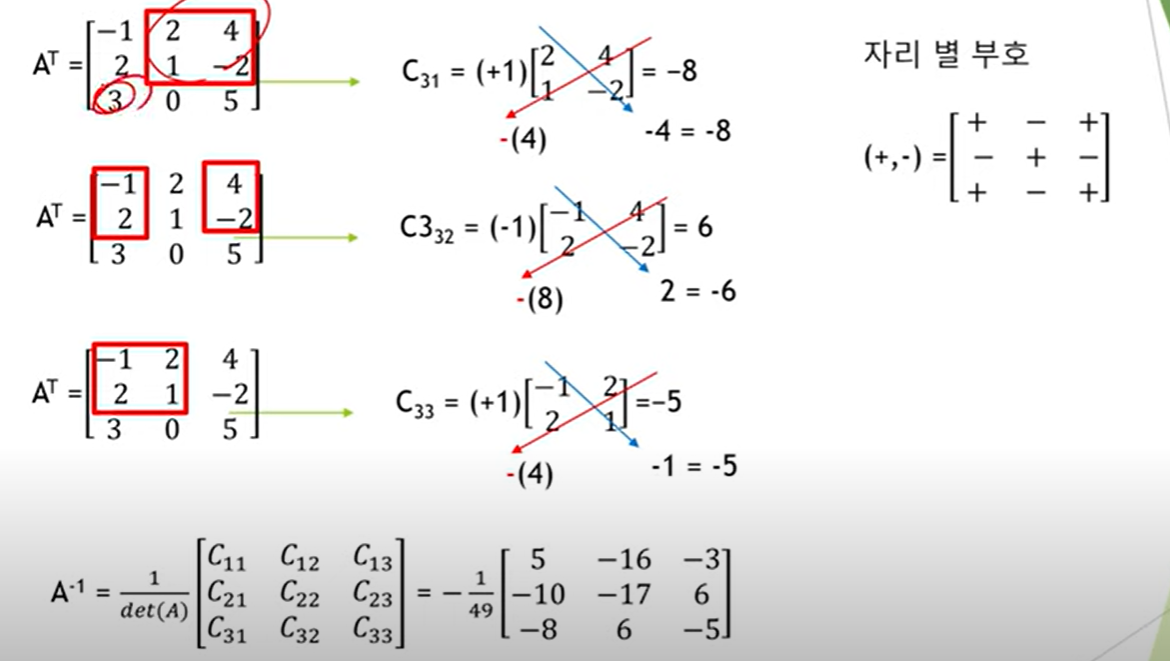
출처: https://www.youtube.com/watch?v=kJgVYO3fCCQ
역행렬 교환법칙 증명
A행렬과 A역행렬을 곱하면 항등원인 I가 나온다.
반대로 A역행렬 x A행렬을 해도 마찬가지로 항등원 I가 나온다.
1/detA = 1/(a11C11 + a12C12 + a1nC1n)(or a21C21 + a22C22 + a2nC2n, or a31C31 + a32C32 + a3nC3n) (그래서 행렬식(detA)이 0이면 역행렬 존재가 불가함. )

크래머 공식

xj는 X의 원소들 x중 j열의 원소 x들을 의미함
detAj는 A행렬중에서 j열만, B행렬의 j열로 바꾸고 나머지 열은 그대로인 행렬임.
( )이 식은 행렬의 곱을 통해서 식을 만들어내고(b1C11 + b2C21 + b3C31)
| |로 묶어준 행렬은 소행렬의 행렬식을 통해서 식을 만들어냄.(b1C11 + b2C21 + b3C31)


과제
https://drive.google.com/file/d/1sAHAxH_lP1I3tUCXCFOOZPoBGbBC5kPj/view
굳이 캡쳐해서 올리는 이유는 저 기호들을 인터넷에 기록하기가 너무 어렵고 번거롭기 때문이다.
출처: https://www.youtube.com/watch?v=83UnOz6HiOY&list=PL127T2Zu76FuVMq1UQnZv9SG-GFIdZfLg&index=3
'📐선형대수학 > 선형대수학' 카테고리의 다른 글
| 수학 각오. (0) | 2023.02.17 |
|---|---|
| 선형대수학(3)(기하와 벡터) (0) | 2023.02.17 |
| 선형대수학(1)(쌩기초) (1) | 2023.02.16 |