<쉘 정렬>
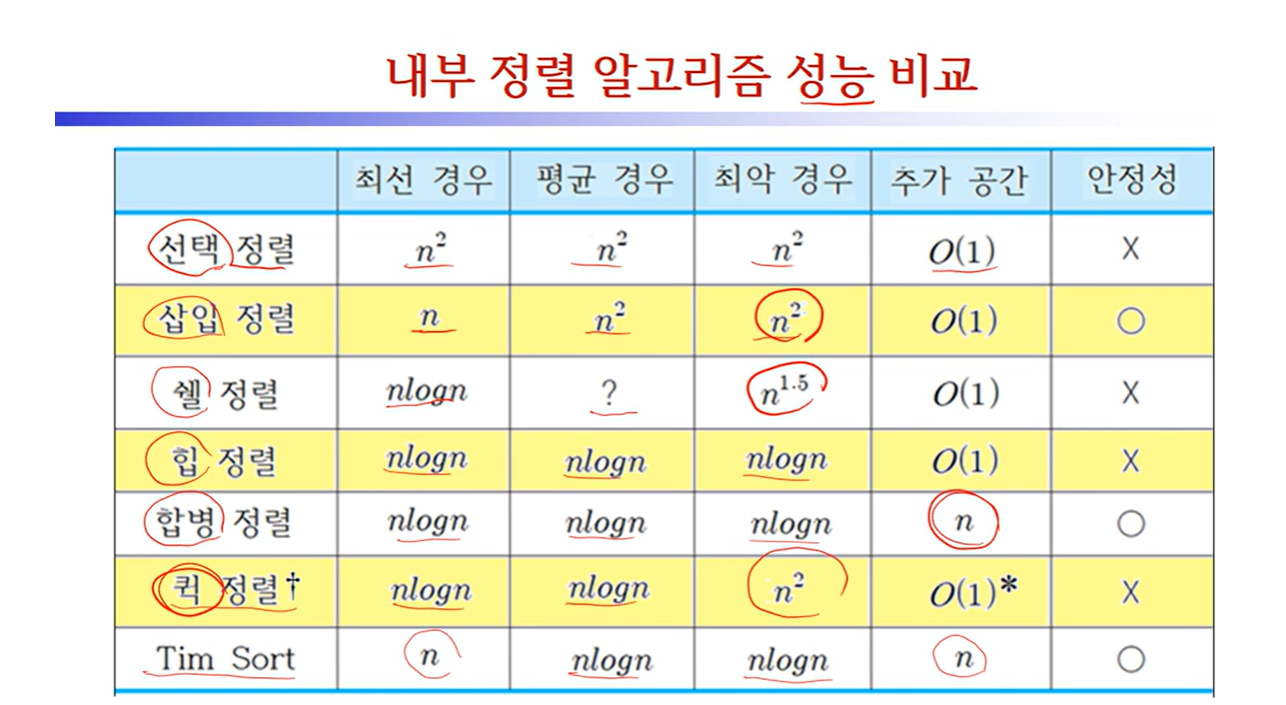
쉘정렬의 평균 시간복잡도는 아직 풀리지 않았다.
가장 좋은 간격을 알아내야하는 것이 선행되어야 하는데 그 방식이 풀리지 않았기 때문이다.
슈도코드
ShellSort
입력: 크기가 n인 배열 A
출력: 정렬된 배열 A
1 for each gap h = [ h0 > h1 > ... > hk=1 ] // 큰 gap부터 차례로
2 for i = h to n-1 {
3 CurrentElement=A[i];
4 j = 1;
5 while(j >= h) and (A[j-h] > CurrentElement) {
6 A[j] = A[j-h];
7 j = j - h;
}
8 A[j] = CurrentElement;
}
9 return 배열 A
h 라는 간격을 정한 후, 각각 묶어준다. lin1
묶어주고 난 h0, h1, ...hk 각각 안에서 삽입정렬 실시. line 2~8
i라는 값의 간격이 1개라면, 묶음 1번 삽입정렬.
i라는 값의 간격이 2개라면, 묶음 2개. 각 삽입정렬 실시. (한번 앞에서 했더라도 또 그 묶음포함 2번하게 되는 것)
(ex)
i = 5 i=0과의 간격에서 한 번 삽입정렬 실시
i = 10 i=5과의 간격 그리고 (i=5, i=0 간격) 각 두번 삽입정렬 실시
간격이 1이라면 삽입정렬 계산과 과정 동일하다.
그런데 굳이 h라는 간격을 통해 쉘 정렬을 해주는 이유는
삽입정렬은 미리 부분적으로 정렬된 데이터를 사용하면, 계산 시간이 많이 줄어들기 때문이다.
<특징>
1. 삽입 정렬을 개선한 알고리즘이다.
2. 중간 크기의 데이터를 정렬하는데 좋은 성능을 보인다.
3. 정렬 알고리즘을 하드웨어로 구현하는데 사용된다.
4. 비안정적 정렬이다.
<힙 정렬>
1. 힙구조를 만든다. (모든 자식을 두개 온전히 가진 노드만을 서로 비교 하여 각 자리에 큰 값들 넣기)
(가장 위의 루트에는 제일 큰 값을 넣는다.)
2. 정렬시작(가장 위에 있는 루트 값과 마지막 자식 노드 값의 자리를 바꾼다. ㅡ> 제일 큰 값 제외 후 다시 1,2 반복)
시간 복잡도는 O(nlogn)
n-1만큼 각각 값을 비교 해줘야 하고, 힙의 높이는 logn을 넘지 않기 때문에 nlogn의 시간 복잡도를 가짐.
HeapSort 슈도코드
입력: 입력이 A[1]부터 A[n]까지 저장된 배열 A
출력: 정렬된 배열 A
1 배열 A의 숫자에 대해서 힙 자료 구조를 만든다.
2 heapSize = n // 힙의 크기를 조잘하는 변수
3 for i = 1 to n-1
4 A[1] <ㅡ> A[heapSize] // 루트와 힙의 마지막 노드를 교환한다.
5 heapSize = heapSize - 1 // 힙의 크기를 1 감소시킨다.
6 DownHeap() // 위배된 힙 조건을 만족시킨다.
7 return 배열 A
line5 아래로 내보낸 가장 큰 값만 빼고 비교해서 힙 크기를 -1 하는것.
line6 맨 마지막 값을 루트에 올림으로써, heap조건을 위배한 후 다시 heap조건을 만족하게끔 힙 조건 만족시킨다.
<특징>
1. 비안정적 정렬이다.
2. 캐시 메모리의 페이지 부재(page fault)를 많이 야기하여 대용량의 입력엔 사용되지 않는다.
(큰 입력에 대해, DownHeap()을 수행하면 자식노드를 찾아야하므로, 너무 많은 캐시미스 발생)
<정렬 문제의 하한>
하한 : 정렬 문제가 어떤 것이든 이보다 더 빠르게 계산 될 수는 없다.
하한은 Ωnlogn
적어도 숫자의 갯수 n개가 있다면 n-1번의 비교가 필요하다.
n이라는 갯수를 가진 문제의 이파리 수는 n! 이다.
이 숫자들을 정렬하는 결정트리의 높이는 아래와 같은 특징이 있다.
'k개의 이파리(자식 노드)가 있는 이진트리의 높이는 logk보다 크다.'
그러므로 n! 개의 이파리를 가진 결정트리를 가진 결정트리의 높이는 log(n!)보다 크다.
그런데 log(n!) = O(nlogn)이다. (n! = n^n이라 볼수 있다.)
즉, O(nlogn) 보다 빠른 시간복잡도를 가진 비교정렬 알고리즘은 존재하지 않는다.
'📈알고리즘 > 알고리즘' 카테고리의 다른 글
| 휴리스틱 flow shop 사례로 이해해보기 (0) | 2023.05.22 |
|---|---|
| 유전자 알고리즘 이해해보기 (0) | 2023.05.17 |
| 버블정렬, 선택정렬, 삽입정렬 (0) | 2023.05.04 |
| 배낭문제 Knapsack (0) | 2023.04.24 |
| 편집 거리 문제(Edit distance) (0) | 2023.04.20 |