슈도 코드
MatrixChain
입력: 연속된 행렬 A1X A2 X.... An, 단, A1은 d0 X d1, A2는 d1 X d2, .... An은 dn-1 X dn 이다.
출력: 입력의 행렬 곱셈에 필요한 원소 간의 최소 곱셈 횟수
1 for i = 1 to n
2 C[i,i] = 0
3 for L = 1 to n-1 { // L은 부분문제의 크기를 조절하는 인덱스이다.
4 for i = 1 to n - L {
5 j = i + L
6 C[i,j] = ∞ (초기화)
7 for k = i to j-1 {
8 temp = C[i,k] + C[k+1,j] + di-1*dk*dj
9 if (temp < C[i,j])
10 C[i,j] = temp
}
}
}
11 return C[1,n]
<전반적 흐름>

위의 최소 비용 Cij를 구하기 위 어디서 행렬을 크게 끊어줘야 하는가?
즉, 어느 부분에서 끊어줘야 최소 행렬 곱셈이 되는가?
끊어주는 위치에 있는 행렬을 k에 있는 행렬. Ak 라고 명명한다.

k로 한번 잘라준 상태에서
앞 괄호 안의 행렬들의 모임은 Ai ~ Ak = Cik => 자르는 기준인 k는 앞 부분에 포함된다
뒷 괄호 안의 행렬들의 모임은 Ak+1 ~ Aj = Ck+1j
로 각각 정의.
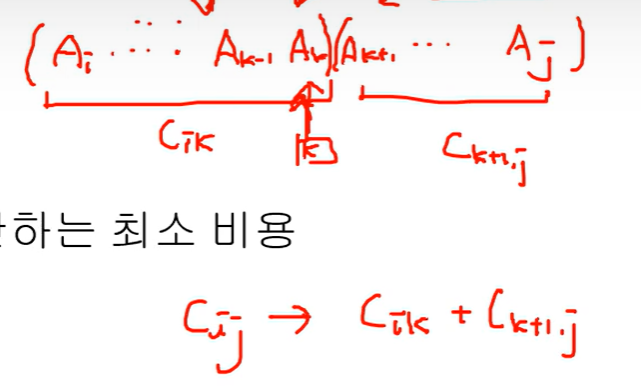
Cij라는 최소비용으로 곱하는 행렬곱셈을 쪼개는 방법은
Cik(Ai~Ak의 총 곱셈 갯수 = di-1)
+ Ck+1j(Ak+1 ~ Aj의 총 곱셈 갯수)
+ di-1*dk*dj (부분문제인 두 행렬(di-1 * dk , dk * dj )을 곱하는데 쓰는 곱셈 갯수)
Cik는 Ai ~ Ak 까지의 곱셈이니...
가운데는 다 소거되고... Ai = di-1 * di // Ak = dk-1 * dk 에서
맨앞과 맨 뒤의 행렬 값인 di-1 * dk 값이 살아남는다. 이 값이 부분 곱셈 갯수
Ck+1j는 Ak+1 ~ Aj 까지의 곱셈이니...
가운데 소거되고 Ak+1 = dk * dk+1 // Aj = dj-1 * dj에서
맨앞과 맨 뒷값인 dk * dj 값이 살아남는다. 이 값이 부분 곱셈 갯수
Cik+ Ck+1j+ di-1*dk*dj
i 는 i ~ n 번 반복.
j = i + 부분문제의 크기(L = 1~n-1 까지 범위 설정가능)
k 는 i ~ i-1(k라는 자르는 구간은 앞 부분문제에 들어가있으니, i부터 반복하지만, j-1까지만 반복가능하다. )

<예제 이해>

출처 : https://www.youtube.com/watch?v=9u0Eb3rvDNY
'📈알고리즘 > 알고리즘' 카테고리의 다른 글
| 배낭문제 Knapsack (0) | 2023.04.24 |
|---|---|
| 편집 거리 문제(Edit distance) (0) | 2023.04.20 |
| 동적 계획 알고리즘(1)[플로이드 모든 쌍 최단 경로 알고리즘] (0) | 2023.04.13 |
| 그리디 알고리즘(7) 허프만 압축 (0) | 2023.04.10 |
| 그리디 알고리즘(6)[작업 스케줄링 JobScheduling] (0) | 2023.04.05 |