입력 : 가중치 그래프 G=(V,E) |V|=n(점의 수), |E|=m(간선의 수)
출력 : 최소 신장 트리 T
1 그래프 G에서 임의의 점 p를 시작점으로 선택하고, D[p]=0 으로 놓는다.
// D[v]는 T에 있는 점 u와 v를 연결하는 간선의 최소 가중치를 저장한다.
ㅡ> D[v]에는 알고리즘이 수행되는 과정 중에서 점v와 T에 속한 점들을 연결하는 간선들 중에서 최소 가중치를 가진 간선의 가중치를 정한다.
2 for (점 p가 아닌 각 점v에 대하여) { // 배열 D의 초기화
3 if( 간선(p,v)가 그래프에 있으면 )
4 D[v] = 간선(p,v)의 가중치
5 else
6 D[v] = ∞
}
7 T = {p} // 초기에 트리 T는 점p만 가진다.
8 while (T에 있는 점의 수 < n) {
9 T에 속하지 않은 각 점 v에 대하여, D[v]가 최소인 점 vmin 과 연결된 간선(u, v)을 T에 추가한다.
단, u는 T에 속한 점이고, 이때 점 vmin도 T에 추가된다.
10 for(T에 속하지 않은 각 점w에 대해서){
11 if(간선(vmin, w)의 가중치 < D[w])
12 D[w] = 간선(vmin, w)의 가중치 // D[w]를 갱신한다.
}
}
13 return T // T는 최소 신장트리다.
2~ 6은 점p와 연결된 점들 각각에만 가중치를 부여, 연결이 안되어 있다면 ∞를 부여
ㅡ> 처음에 p와 연결 안된점은 모두 ∞로 만드는 과정
7 은 다시 기준인 점으로 돌아옴.
8은 T에 아직 속하지 않은 모든 점 v에 대해 반복 의미(T에 처음 속한건 기준인 점p 하나지만, 계속 p와 연결되는 점이 증가)
9는 기준에서 가중치가 제일 작은 점과 간선을 T로 넣는 작업.
신장 트리 T(1.점p, 2. 가중치를 만족하는 점들, 3. 그 사이를 잇는 간선들 ㅡ> 이 세가지의 모임)에
최소 가중치를 가진 점vmin 과 이미 T에 속한 점인 u(p와 계속 선택받아온 점들 중, 제일 최근 T로 들어간 점) 간의 간선을 T에 추가한다.
10~12는 ∞에서 각 간선들을 갱신해 나가는 과정
10: T에 속하지 않은 점인 w의 수만큼 검사
ㅡ>
11:
조건이 if(간선(vmin, w)의 가중치 < D[w])이다.
조건이 성립되면
vmin과 연결되지 않은 w점은 vmin과의 간선이 없기 때문에 계속 ∞를유지한다.
vmin과 연결된 점w 들은 if( 간선길이 <D[w]=∞)를 무조건 만족함.
12:
조건을 만족했으니 간선의 길이로 D[w] 값을 갱신.
그리고 D[w]란, 이미 T에 있는 모든 점들과 임의의 w 한 점의 최단 거리를 의미함. (vmin과 임의의w 한점 간의 간선 가중치를 의미하는 게 아님.)
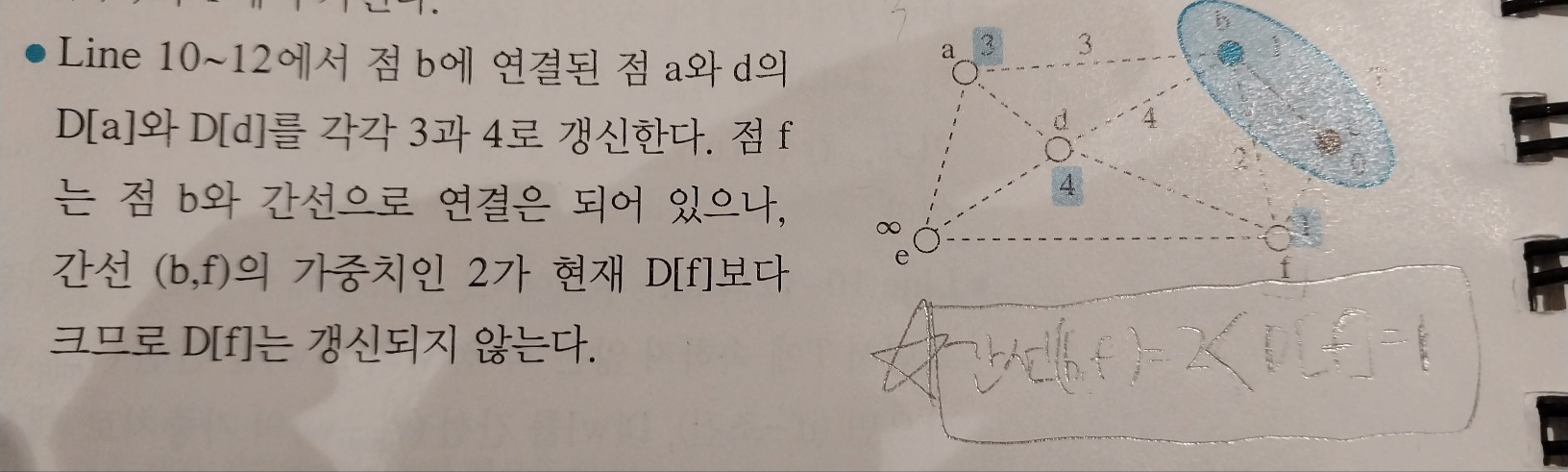
아래처럼 간선의 가중치가 2이고, T점들과의 최단 거리가 1일 경우 if조건문이 성립되지 않을 수 있음.
조건이 성립되지 않는다. 간선(b,f) = 2 > D[f] = 1 이기 때문이다.
이때 조건을 만족하지 못한 간선은 쓰임받지 못하는 선이된다.
그리고 다시 9로 돌아가서 간선으로 바뀐 D[w]값들과 비교하여 최소값으로서 T에 속해질 때를 기다리게 된다.
끝나고 while문 조건인 T에 모든 점들이 들어갈 때까지 위와 같은 과정이 반복되면서 최소 가중치의 선들을 찾는다.
반복문이 두번 쓰였음으로 시간 복잡도는 O(n**2)이다.
위의 수도코드를 처음에 이해하기가 쉽지않다. 아래처럼 풀어서 적은 글을 가져와봤다.
프림 알고리즘은 아래의 순서대로 작동한다:
- 그래프에서 하나의 꼭짓점을 선택하여 트리를 만든다.
- 그래프의 모든 변이 들어 있는 집합을 만든다.
- 모든 꼭짓점이 트리에 포함되어 있지 않은 동안
- 트리와 연결된 변 가운데 트리 속의 두 꼭짓점을 연결하지 않는 가장 가중치가 작은 변을 트리에 추가한다.
알고리즘이 종료됐을 때 만들어진 트리는 최소 비용 신장트리가 된다
- 트리 정의 -
그래프 이론에서 나무 그래프(영어: tree graph 트리 그래프[*]) 또는 단순히 나무는 순환을 갖지 않는 연결 그래프이다.
- 신장트리 정의 -
그래프 이론에서 신장 부분 그래프(身長部分graph, 영어: spanning subgraph 스패닝 서브그래프[*]) 또는 생성 부분 그래프(生成部分graph)는 모든 꼭짓점을 포함하는 부분 그래프이다.
'📈알고리즘 > 알고리즘' 카테고리의 다른 글
| 그리디 알고리즘(4)[ 부분 배낭 문제(Fractional Knapsa) ] (0) | 2023.04.05 |
|---|---|
| 그리디 알고리즘(3)[ShortestPath(G,s)] (0) | 2023.04.03 |
| 그리디 알고리즘(1)[KruskalMST 구현(by js)] (0) | 2023.03.30 |
| 정복 알고리즘-선택문제 (0) | 2023.03.27 |
| 퀵정렬 이해하기 (0) | 2023.03.20 |